Econometrics Basics for Interviews

In this blog, we have tried to explain multicollinearity, autocorrelation, and heteroscedasticity clearly.

Why are there error terms in a model?

You must have noticed the presence of an error term (ϵ, greek letter epsilon) in every statistical model. Below are the reasons for it:

1. Usually, it is not possible to consider all the independent variables in a model. Thus, error terms account for the variation due to variables that are not included in the model. 
2. It is also possible that there are errors in measurements of response and explanatory variables.

For the upcoming sections of this blog, we strongly recommend you to read our previous blog on Linear Regression if you haven’t already 😛

The three important assumptions of linear regression are no multicollinearity, no autocorrelation, and no heteroscedasticity. We will now study the causes, consequences, and detection of each of these assumptions.

Multicollinearity

Multicollinearity is a sample phenomenon. It refers to the existence of a linear relationship among explanatory variables. it is always about the severity of presence rather than simple presence because we are going to encounter it in most of the samples.

Causes

1. Often economic data tend to move together.
2. Choice of the sample.
3. Specification of the model.

Consequences

1. Estimates have large standard errors if multicollinearity is present in the data. Thus precision of estimates declines.
2. The t-ratios would become insignificant which would lead to the dropping of incorrect variables from the model.
3. The estimated coefficients become sensitive to sample data.
4. It is almost impossible to estimate parameters in the case of perfect multicollinearity.

Test / detection

A. Frisch confluence analysis

Regress all X(independent variables) on Y(dependent variable). Choose X with the highest R-squared value and add the X having the second-highest R-squared value in the model. Then the addition of a new variable can be termed as follows:

1. Useful, if there is a significant increase in the R-squared value but insignificant in the coefficient estimates of the model.
2. Superfluous, if there is a significant decline in R-squared value and insignificant change in the coefficient estimates of the model.
3. Detrimental, if there is a significant change in the coefficient estimates. This would imply the presence of multicollinearity.

B. Farrar Glauber test

1. Chi-square test to detect the presence of multicollinearity
2. F-Test to locate multicollinearity
3. T-test to detect the pattern of multiplication

C. VIF or Variance Inflation Factor is also used for the detection of multicollinearity. A VIF value of greater than 10 indicates severe multicollinearity.

Autocorrelation

Also known as serial correlation, it is a phenomenon wherein the error terms are correlated. It is very common in time-series data.

Causes

1. Omitted variables
2. Autoregressive lag model
3. Errors in measurement
4. Data manipulation i.e. smoothening of data

Consequences

1. OLSE(Ordinary Least Square Estimates) grossly underestimate the variance of the error terms although they are unbiased
2. The variance of the coefficient estimates is underestimated
3. Large t-values imply incorrect conclusions

Test / detection

A. Von Neumann Ratio test

It uses z-test to check for the presence of autocorrelation. The null hypothesis is that there is no autocorrelation in the data. The ratio defined by Z below is called the Von Neumann Ratio. For large n (sample size), Z is approximately normal with

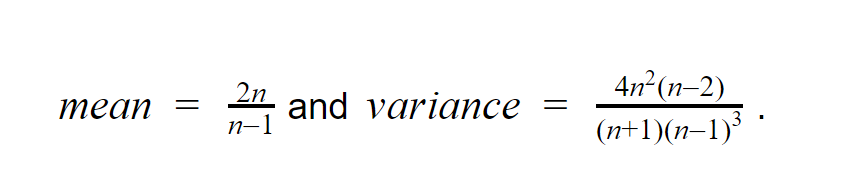
B. Durbin Watson test

The assumptions of the Durbin Watson test are stated as follows:

1. There should be no missing observation in the data
2. Necessary intercept term in the model
3. The error terms follow the first-order autoregressive scheme
4. Lagged values of Y(dependent variable) should not be present in the model

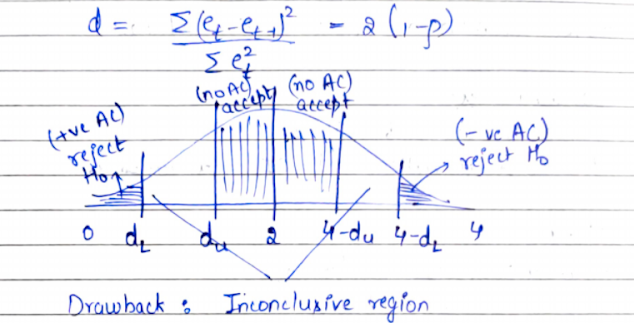
The only drawback of this test is the presence of an inconclusive region.

Heteroscedasticity

When the variance of the error terms is not constant then the model is said to have the presence of heteroscedasticity.

Causes

1. Common error learning models
2. Common in discretionary income models
3. Improvement in data collection techniques over a period of time
4. Due to the presence of outliers in data
5. Misspecification of the model
6. Skewness in the distribution of regressors
7. More common in cross-sectional data

Consequences

1. Coefficient estimates are not MVUE (Minimum Variance Unbiased Estimates)
2. Hence t statistic and confidence interval get affected

Tests

The tests assume the null hypothesis of homoscedasticity i.e. constant variance. Thus, if we reject the null hypothesis, then we conclude that heteroscedasticity is present in the data.

A. Spearman’s rank correlation

We use the rank correlation between the absolute value of errors and each independent variable to compute the t statistic. If the computed value of t is more than the tabulated value, then we assume that heteroscedasticity is present in the data.

B. Goldfeld and Quandt test

Assumption: For applying this test, the number of observations in data should be at least double the number of variables in the model.

The procedure is to arrange the data in ascending order and leave the middle c observations (Here, c is a pre-decided number). Then run regression on two samples obtained i.e. the top and the bottom sample and let e1 square and e2 square be SSE (Sum of Squares due to errors) of two samples. We then compute the F-ratio. In general, large F values typically indicate that the variances are different i.e. heteroscedasticity is present in the data.

Do well! 

Cheers!

You can find some of the resources that helped us here.

For any query about the process or suggestion about topics that we can talk about in future, you can reach out to us on Linkedin.

Kanika Tayal & Anubhav Dubey